Властивості паралельних прямих

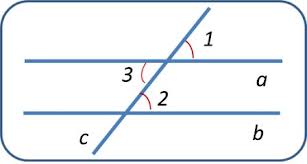
Теорема 1. Якщо дві паралельні прямі перетнуті третьою прямою, то:
1) внутрішні різносторонні кути рівні;
2) сума внутрішніх односторонніх кутів дорівнює ;
3) зовнішні різносторонні кути рівні;
4) сума зовнішніх односторонніх кутів дорівнює ;
5) відповідні кути рівні.

Теорема 2. Якщо пряма перпендикулярна до однієї з паралельних прямих, то вона перпендикулярна і до другої.
Теорема 3. Через точку, що не лежить на прямій, можна провести пряму, паралельну даній.
Об’єднуючи це твердження з аксіомою IX, отримуємо: через точку, що не лежить на прямій, можна провести пряму, паралельну даній, причому тільки одну.
Ознаки паралельності прямих
Теорема 1. Якщо при перетині двох прямих третьою виконується хоча б одна з таких умов:
а) внутрішні різносторонні кути рівні;
б) сума внутрішніх односторонніх кутів дорівнює ;
в) зовнішні різносторонні кути рівні;
г) сума зовнішніх односторонніх кутів дорівнює ;
д) відповідні кути рівні,— то прямі паралельні.
Теорема 2. Дві прямі, паралельні третій, паралельні одна одній.
Теорема 3. Дві прямі, перпендикулярні до третьої, паралельні одна одній.

Паралельні прямі, їх властивості

Дві прямі називаються паралельними, якщо вони не перетинаються.
Два відрізка називаються паралельними, якщо вони лежать на паралельних прямих.

Через точку, що не лежить на даній прямій, можна провести на площині пряму, паралельну до даної, і тільки одну. Це твердження є основною властивістю паралельних прямих:

Дві прямі, кожна з яких паралельна третій прямій, паралельні між собою.

Якщо пряма перетинає одну з паралельних прямих, то вона перетинає і другу пряму.
Історичні відомості.

Основна властивість паралельних прямих — це п’ятий постулат Евкліда. Постулат — це математичне твердження, яке приймається без доведення. Цей постулат першої книги «Начал» Евкліда безуспішно намагалися довести вчені протягом двох тисяч років, і ці спроби привели до відкриття Лобачевским у першій половині 19 століття геометрії неевклідової, яку було названо геометрією Лобачевского.

Наочним прикладом паралельних прямих можуть слугувати рельси залізниці.